(五) 分支限界算法

Word count: 3.3kReading time: 12 min

 2021/06/28   Share

分支限界法：广(宽)度优先搜索 + 剪枝。

一、基本思想

1.1 分支限界法与回溯法

与回溯法的异同

相同点：与回溯法一样，分支限界也是搜索一个解空间，而这个解空间通常组织成一棵树(常见的树结构：子集树和排列树)。
- 解题步骤都基本一样的：定义解空间、确定解空间结构、深度/广度优先搜索 + 剪枝
不同点：
- 搜索策略：回溯以深度优先搜索树，而分支限界常常以广度优先或最小耗费(最大效益)优先的方法搜索问题的解空间树。
- 求解目标：回溯法的求解目标一般是找出解空间树中满足约束条件的所有解。分支限界法的求解目标则是找出满足约束条件的一个解，或是在满足约束条件的解中找出在某种意义下的最优解。

充分利用限界函数和约束函数来剪去无效的枝并把搜索集中在可以得到解的分支上。

1.2 分支界限法的要素

1.2.1 限界函数/界限函数

设立限界函数，其函数值是以该结点为根的搜索树中的所有可行解的目标函数值的上/下界。
记录已得的最优可行解，其值是当时已经得到的可行解的目标函数的最大/小值(初始值可以置为 ∞ 或用某种启发式方法得到)。
搜索中停止分支的依据：如果某个结点不满足约束条件或者其限界函数的得出的上/下界小/大于当时的最优可行解，则不再分支，向上回溯到父结点。
最优可行解的更新：如果目标函数值为正数，初值可以设为0。在搜索中如得到一个可行解，计算可行解的目标函数值，如果这个值大于当时记录的最优可行解，就将这个值记录作为新的解。

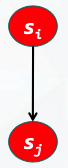
目标函数是求最大值:
- 设计上界限界函数ub，若 si 是 sj 的双亲结点，应满足 ub(si) ≥ ub(sj)；
- 当找到一个可行解 ub(sk) 后，将所有小于 ub(sk) 的结点剪枝。
目标函数是求最小值:
- 设计下界限界函数lb，若 si 是 sj 的双亲结点，应满足 lb(si) ≤ lb(sj)；
- 当找到一个可行解 lb(sk) 后，将所有大于 lb(sk) 的结点剪枝。

1.2.2 活结点表

不同于回溯法，在分支限界法中，每一个活结点只有一次机会成为扩展结点。活结点一旦成为扩展结点，就一次性产生其所有儿子结点。在这些儿子结点中，通过剪枝函数将导致不可行解或导致非最优解的儿子结点舍弃，其余儿子结点被加入活结点表中。

此后，从活结点表中取下一结点成为当前扩展结点，并重复上述结点扩展过程。这个过程一直持续到找到所需的解或活结点表为空时为止。

不同的活结点表形成不同的分枝限界法，分为：FIFO分支限界法、LIFO分支限界法和LC(least cost)分支限界法。三种不同的活结点表，规定了从活结点表中选取下一个E-结点的不同次序。

FIFO分支限界法的活结点表是队列，按照队列先进先出（FIFO）原则选取下一个节点为扩展节点。
LIFO分支限界法的活结点表是堆栈，按照堆栈先进后出（LIFO）原则选取下一个节点为扩展节点。
LC分支限界法的活结点表是优先权队列，按照优先队列中规定的优先权选取具有最高优先级的活结点成为新的E-结点。
- 最大优先队列（最大堆）：体现最大效益优先
- 最小优先队列（最小堆）：体现最小费用优先

在LIFO和FIFO分支限界法中，对下一个E-结点的选择规则死板，在某种意义上是盲目的搜索。

LC分支限界法在选择活结点时根据活结点的优先权来选择下一代活结点。结点优先权定义为：“在其分支下搜索一个答案状态需要花费的代价，代价越小，越优先”。

分枝限界法的特性：

时间性能：最坏的情况要搜索整个解空间，是复杂度是指数型。但如果启发式信息强且剪枝处理得当，平均性能往往很好。
空间性能：优先队列往往需要较大的空间开销。

二、基本步骤

2.1 步骤

针对所给问题，定义问题的解空间
对解空间进行组织，确定易于搜索的解空间结构(树或图)
设计合适的限界函数
选定节点扩展策略，组织活结点表，使用限界函数来避免那些不能得到解的子空间。

下面来看一下存在性问题、最优化问题中的代价函数和限界函数。

2.2 存在性问题的分支限界法 — 代价函数

代价的函数 c(·)：表示从根结点搜索到 X，以及在 X 之下搜索到一个答案状态所需的代价。
- 若 X 是答案结点，则 c(X) 是从根结点到 X 的搜索代价；
- 若 X 不是答案结点且子树X上不含任何答案结点，则 c(X) = ∞ ；
- 若 X 不是答案结点但子树 X 上包含答案结点，则 c(X) 等于子树 X 上具有最小搜索代价的答案结点的代价。

代价函数如同一个“有智力的”排序函数，基于其值选取下一个 E- 结点往往可以加快到达一答案结点的速度。

相对代价的函数 g(·) ：衡量子树X下搜索到一个答案状态所需的代价。
- 对任意结点 X ，可用两种标准来量度一个结点 X 的相对代价：
  - ① 在生成一个答案结点之前，子树 X 上需要生成的结点数目；
  - ② 在子树 X 上，离 X 最近的答案结点到 X 的路径长度。

代价是答案结点到根节点的搜索代价，相对代价是子树下的答案结点到子树根X的搜索代价。

由定义知，直接求 c(·) 和 g(·) 是十分困难。

相对代价的估计函数 ĝ(.) ：用于估计在 X 下搜索到一个答案状态所需的代价。
- ĝ(·) 需要视具体问题而定！一般地，假定 (X) 满足如下特性：如果 Y 是 X 的孩子，则有 (Y) ≤ (X)。
代价的估计函数 ĉ(.)
- ĉ(X) 是代价估计函数，它由两部分组成：从根到 X 的代价 f(X) 和从 X 到答案结点的估计代价 (X)，即 ĉ(X) = f(X) + ĝ(X)。
- 一般而言：
  - f(X) = X 在树中的层次；
  - ĝ(.) 根据具体问题确定。

LC检索(即最小成本检索)：总是选取 ĉ(.) 值最小的活结点为下一个E结点。

若令 f(X) ≡ 0 时， LC检索退化为DFS搜索；
若令 ĝ(·) ≡ 0 时，LC检索退化为BFS搜索。

2.3 求最优解的分支限界法 — 代价函数、界函数

重新界定结点代价的含义。选择与目标函数有关的度量值

若 X 是答案结点，则 c(X) 即是这个解的目标函数值；
若 X 是叶子结点且非解，则 c(X) = ∞ 或 -∞；
若 X 是是中间结点，则 c(X) 等于子树 X 中结点的最优目标值。

不直接求c(X)。

限界函数：上界函数 u(·) 和下界函数 ĉ(·) 分别是代价函数 c(·) 的上界和下界函数。

对任一结点X，总有 ĉ(X) ≤ c(X) ≤ u(X)
限界函数的意义对最优解状态的目标函数值的范围进行界定，实现剪枝。

2.4 回溯法和分支限界法的区别

	对解空间树的搜索方式	存储结点的常用数据结构	结点存储特性	求解目标
回溯法	深度优先搜索	递归；非递归时使用堆栈	活结点的所有可行子结点被遍历后才被从栈中弹出（结点可能多次成为扩展结点）	找出解空间树中满足约束条件的所有解
分支限界法	广度优先或最小消耗优先搜索	三种：队列、堆栈、优先队列	每个活结点只有一次成为扩展结点的机会	找出满足约束条件的一个解，或是在满足约束条件的解中找出在某种意义下的最优解。

三、程序设计

一般的算法设计模式如下：

3.1 存在性问题 — 分枝限界

存在性问题 — 分枝限界法算法框架（C++）

//树结点的数据结构
//状态空间树采用树的双亲表示法，parent是指向其双亲的指针
template <class T> 
struct Node{
    T cost;
    Node* parent;   
};

/* 活结点表的类型记为LiveList ：FIFO/LIFO/优选权队列 */

template<class T> void BranchBound(Node<T>* t)  // t是指向空间树的根结点
{
    LiveList<Node<T>* > lst(mSize);   // lst为活结点表，元素指向树结点
    Node<T> *x,*E=t;                  // E为指向扩展结点的指针，初始指向t
    do {   // 以下描述中不区分指针与其所指示的结点
       for(对结点E的每个不受限的孩子){
           x=new Node; x->parent=E; //构造E的孩子结点x
           if ( x是一个答案结点 ){
             输出从x到t的一条路径；
             return;      // 输出第一个解后算法终止
           }
           lst.Append(x); // 孩子结点x进活结点表
       }
       if(lst.IsEmpty()){
           cout << “没有答案结点”；
           return；  // 搜索失败终止
       } 
       lst.Serve(E);      // 从表中输出一个活结点为E-结点
    }while（1）；
}

3.2 最优解问题 — 分枝限界

最优解问题 — 分枝限界法算法框架（基于剪枝的FIFO、LC分枝限界求最小值 C++）

/*
 * 提示：目标函数cost(X)、代价函数c(X)、上界函数u(.)和下界函数ĉ(.)
 * U的值可以按下列原则修正：
      如果X是答案结点，cost(X)是X所代表的可行解的目标函数值，u(X)是该子树上最小代价答案结点代价的上界值，则U=min{cost(X), u(X)+ε, U}；
      如果X代表部分向量，则U=min{u(X)+ε, U}。
 * 使用ĉ(X)≥U 剪除多余分枝。
 */
template<class T>
Node<T>* LCBB(Node<T>* t,  T& U) //t为根，U为上界变量
{  
    LiveList<Node<T>* > lst(mSize);  //lst为优先权队列
    Node<T> *ans=NULL, *x, E=*t; 
    do {
      for( 对结点E的每个孩子){  //所有满足约束条件的孩子
          x=new Node; x->parent=E;  //构造E的孩子结点x
          if ( ĉ(x)<U){ //若x子树未被限界函数剪枝
             lst.Append(x); 
             //以下修正U
             if ( x是答案结点 && cost(x)<U )
                if ( u(x)+ε < cost(x) ) U = u(x)+ε; 
                else { U = cost(x); ans=x;}
             else if(u(x)+ε<U) U=u(x)+ε;
          }
      }
      //---------如果是FIFO分支限界法----------      
      do{
         if(lst.IsEmpty()) return ans;       
         lst.Serve(E);                   
      } while (ĉ(E)≥U );    
      //---------如果是FIFO分支限界法----------
      
      //---------如果是LC分支限界法----------
      if(!lst.IsEmpty()){
         lst.Serve(E);  //从队列中取扩展结点E
         if (ĉ(E)≥U) return ans;    //若^c(E)≥U，则算法结束
      }
      else return ans;   //若队列为空，则算法结束
      //---------如果是LC分支限界法----------
    }while（1）；
}

四、经典运用

单源最短路径问题
装载问题
布线问题
0-1背包问题
最大团问题
TSP问题(旅行售货员问题、货郎担问题、邮路问题)
电路板排列问题
批处理作业调度问题

举例：优先队列式分支限界法解 —— 装载问题

解装载问题的优先队列式分支限界法用最大优先队列存储活结点表。活结点x在优先队列中的优先级定义为从根结点到结点x的路径所相应的载重量再加上剩余集装箱的重量之和。
优先队列中优先级最大的活结点成为下一个扩展结点。以结点x为根的子树中所有结点相应的路径的载重量不超过它的优先级。子集树中叶结点所相应的载重量与其优先级相同。
在优先队列式分支限界法中，一旦有一个叶结点成为当前扩展结点，则可以断言该叶结点所相应的解即为最优解。此时可终止算法。

Author：Tenloy

原文链接：https://tenloy.github.io/2021/06/28/branch-bound.html

发表日期：2021.06.28 , 4:40 AM

更新日期：2024.04.07 , 8:02 PM

Next Post

(六) 概率算法
Previous Post

(四) 回溯法(试探算法)

CATALOG

一、基本思想
1. 1.1 分支限界法与回溯法
2. 1.2 分支界限法的要素
  1. 1.2.1 限界函数/界限函数
  2. 1.2.2 活结点表
二、基本步骤
三、程序设计
1. 3.1 存在性问题 — 分枝限界
2. 3.2 最优解问题 — 分枝限界
四、经典运用

