搜索
Tenloy's Blog

(一) 分治算法及减治、变治算法

Word count: 2.6kReading time: 9 min
2021/06/20 Share

一、基本思想

字面上的解释是“分而治之”，就是将一个规模为N的问题分解为K个规模较小的子问题( 反复分解直到问题小到可直接求解为止)，使这些子问题相互独立可分别求解，再将k个子问题的解合并成原问题的解。

  • 这些子问题相互独立且与原问题性质相同(规模一般也相同)。只要求出子问题的解，合并就可得到原问题的解。

在分治法中，子问题的解法通常与原问题相同。这自然导致 递归过程。

  • 分治与递归像一对孪生兄弟，经常同时应用在算法设计之中，并由此产生许多高效算法。

二、适用情况

分治法能解决的问题一般具有以下4个特征：

  • 当问题的规模缩小到一定的程度就可以容易地解决。
    • 该特征是绝大多数问题都可以满足的，因为问题的计算复杂性一般是随着问题规模的增加而增加；
  • 问题可以分解为若干个规模较小的问题，即该问题具有最优子结构性质。
    • 该特征是应用分治法的前提，它也是大多数问题可以满足的，此特征反映了递归思想的应用；
  • 利用该问题分解出的子问题的解可以合并为该问题的解（关键）；
    • 该特征是关键，能否利用分治法完全取决于问题是否具有第三条特征，如果具备了第一条和第二条特征，而不具备第三条特征，则可以考虑用贪心法或动态规划法。
  • 各个子问题是相互独立的，即子问题之间不包含公共的子问题。
    • 该特征涉及到分治法的效率，如果各子问题是不独立的则分治法要做许多不必要的工作，重复地解公共的子问题，此时虽然可用分治法，但一般用动态规划法较好。

这个思想是很多高效算法的基础，在各种排序方法中，如：归并排序、堆排序、快速排序等，都存在有分治的思想。还有傅立叶变换(快速傅立叶变换)等

三、基本步骤

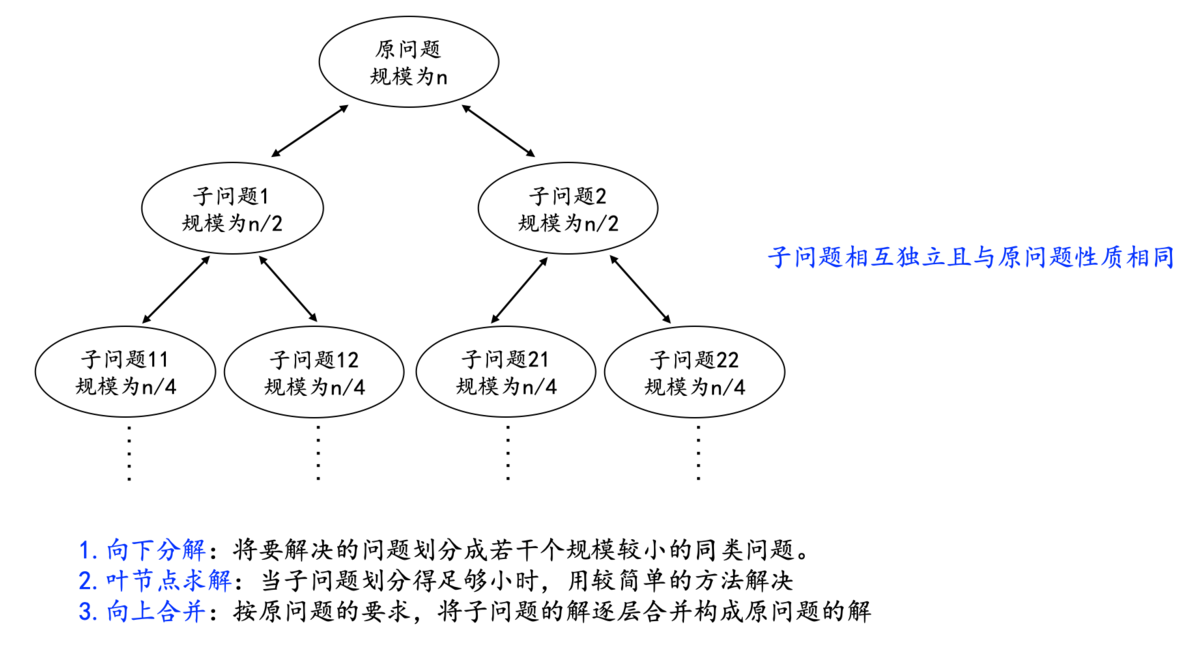
  1. 分解，将要解决的问题划分成若干个规模较小的同类问题
  2. 求解，当子问题划分得足够小时，用较简单的方法解决
  3. 合并，按原问题的要求，将子问题的解逐层合并构成原问题的解
img

要点：

  • 分几个？子问题规模多大？ 最好使子问题的规模大致相同。即将一个问题分成大小相等的 k 个子问题的处理方法是行之有效的。
  • 子问题如何求解?
  • 合并原问题的解?
  • 分析时间复杂性

四、程序设计

4.1 依据分治法设计程序时的思维过程

实际上就是类似于数学归纳法，找到解决本问题的求解方程公式，然后根据方程公式设计递归程序。

  1. 一定是先找到最小问题规模时的求解方法
  2. 然后考虑随着问题规模增大时的求解方法
  3. 找到求解的递归函数式后（各种规模或因子），设计递归程序即可。
    分治的算法思想与递归往往是相伴而生的

4.2 一般的算法设计模式如下

1
2
3
4
5
6
7
8
9
10
11
12
13
Divide-and-Conquer(P)

    if |P|≤n0
    then return(ADHOC(P))

    将P分解为较小的子问题 P1 ,P2 ,…,Pk

    for i←1 to k
        do yi ← Divide-and-Conquer(Pi) △ 递归解决Pi

    T ← MERGE(y1,y2,…,yk) △ 合并子问题

    return(T)

其中:

  • |P| 表示问题P的规模；
  • n0 为一阈值，表示当问题P的规模不超过n0时，问题已容易直接解出，不必再继续分解。
  • ADHOC(P) 是该分治法中的基本子算法，用于直接解小规模的问题P。因此，当P的规模不超过n0时直接用算法ADHOC(P)求解。
  • 算法 MERGE(y1,y2,…,yk) 是该分治法中的合并子算法，用于将P的子问题 P1 ,P2 ,…,Pk 的相应的解y1,y2,…,yk 合并为P的解。

4.3 复杂度

  • 一个分治法将规模为n的问题分成k个规模为n／m的子问题去解。
    • 设分解阀值n0=1，且 adhoc 解规模为1的问题耗费1个单位时间。
    • 再设将原问题分解为k个子问题以及用 merge 将k个子问题的解合并为原问题的解需用f(n)个单位时间。
    • 用T(n)表示该分治法解规模为|P|=n的问题所需的计算时间，则有：T(n) = kT(n/m)+f(n)
  • 通过迭代法求得方程的解：
    • 递归方程及其解只给出n等于m的方幂时T(n)的值，但是如果认为T(n)足够平滑，那么由n等于m的方幂时T(n)的值可以估计T(n)的增长速度。通常假定T(n)是单调上升，从而当 mi ≤ n < mi+1时，T(mi) ≤ T(n) < T(mi+1)。

五、经典运用

  • 二分查找
  • 合并(归并)排序
  • 快速排序
  • 最大子段和
  • 最近对
  • 凸包
  • 汉诺塔
  • 大数相乘问题
  • 比赛日程安排
  • 寻找假币问题
  • Strassen矩阵乘法
  • 棋盘覆盖
  • 线性时间选择
  • …
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
//示例代码：二分查找
#include <stdio.h>
 
int bin_search(int A[], int n, int key)
{
    int low = 0, high = 0, mid = 0;
    high = n - 1;
    while (low <= high) {
        mid = (low + high) / 2;
        if (A[mid] == key) { //查找成功，返回mid
            return mid;
        }
        if (A[mid] < key) { //在后半序列中查找
            low = mid + 1;
        }
        if (A[mid] > key) { //在前半序列中查找
            high = mid - 1;
        }
    }
    return -1; //查找失败
}
 
int main(int argc, const char * argv[]) {
    // insert code here...
    int A[10] = {2, 3, 5, 7, 8, 10, 12, 15, 19, 21};
    int i = 0, n = 0, addr = 0;
    printf("The contents of the Array A[10] are\n");
    for (i = 0; i < 10; i++) {
        printf("%d ",A[i]); //显示数组A中的内容
    }
    printf("\nPlease input a interger for search\n");
    scanf("%d", &n); //输入待查找得元素
    addr = bin_search(A, 10, n); //折半查找，返回该元素在数组中的下标
    if (-1 != addr) {
        printf("%d is at the %dth unit is array A\n", n, addr);
    }else{
        printf("There is no %d in array A\n", n); //查找失败
    }
    getchar();
     
    return 0;
}

六、补充：减治、变治算法

6.1 减治算法

6.1.1 概述

将规模为n的问题递减为n-1/n-2的子问题，反复递减后对子问题分别求解，再建立子问题的解与原问题的解的关系

分治法与减治法：

  • 相同点：关键都是将父问题划分为子问题
  • 区别是：分治法最后一般需要将子问题合并求原问题的解，而减治法一般情况是：父问题的解便存在于某个子问题的解中。
    • 分治和减治不同的地方是 分治分开 的两边都要治理，但 减治减掉 的那部分就不需要了。

是一种一般性的算法设计技术，它利用了一个问题给定实例的解和同样问题较小实例的解之间的关系。一旦建立了这样一种关系，我们既可以自顶至下(递归)也可以自底至上地运用它(非递归)。

减治法有3种主要的变种：

  • 减一个常量，常常是减1(例如插入排序)
    • n个元素我们减去C个元素（C是一个正整数）
  • 减一个常因子，常常是减去因子2(例如折半查找)
    • 将集合的元素一分为二或者分成多份。比如将 n-1 改为 n/2。
  • 减可变规模(例如欧几里得算法)
    • 集合中每次减去的规模不一样,比如有n个元素的集合，我第一次减去一个元素成为 n-1 第二次减去了 n/2 的元素成为 (n-1)/2。

6.1.2 经典运用

  • 查找（折半、二叉查找树）
  • 选择问题
  • 插入排序
  • 堆排序
  • 假币问题

6.2 变治算法

6.2.1 概述

所谓变治，就是基于”变换”的方法，首先把问题的实例变得容易求解，然后进行求解，通常，对问题的变换方式有三种：

  1. 实例化简：变为同样问题的一个更简单的实例；
  2. 改变表现：变为同样实例的不同表现；
  3. 问题化简：变为另一个已知算法的问题的实例

这个方法的思路类似于数学建模的思路，将生活的问题进行简单的抽象，以便对此进行研究，举一个简单的例子：

  • 在操场（欧几里得平面）上有n>=3个人，每个人都有唯一一位最近的邻居，他们手上拿着1块奶油块，收到信号后，都会把派扔向他最近的邻居。假设n是奇数，而且每个人都可以100%命中对方，请判断对错：每次至少有一个人不会被奶油派击中。
  • 这个问题应该是正确的，我们来以3个人A，B,C举例，假如A与B的距离为c，B与C的距离为a，C与A的距离为b，那么如果每个人都会被扔到那么他们的距离关系应当满足 c<a, b<c, a<c; 显然我们发现这是存在前后矛盾的因此我们可以断定每次至少有一个人不会被奶油派击中是正确的。

这是将实际问题抽象的一个例子，将人抽象成点，将距离抽象成线的长度，并且利用反证法来证明这个假设。

6.1.2 经典运用

基于这种思想的算法也有很多，如：

  • 预排序（把无序变为有序，然后处理）
  • 高斯消去法（把方程组经过初等变换，得到具有特殊性质的方程组）
  • 堆和堆排序（利用最大/小堆总是找到最大/小值）

Author：Tenloy

原文链接：https://tenloy.github.io/2021/06/20/divide-and-conquer.html

发表日期：2021.06.20 , 9:40 AM

更新日期：2024.04.07 , 8:02 PM

版权声明：本文采用Crative Commons 4.0 许可协议进行许可

CATALOG
  1. 一、基本思想
  2. 二、适用情况
  3. 三、基本步骤
  4. 四、程序设计
    1. 4.1 依据分治法设计程序时的思维过程
    2. 4.2 一般的算法设计模式如下
    3. 4.3 复杂度
  5. 五、经典运用
  6. 六、补充：减治、变治算法
    1. 6.1 减治算法
      1. 6.1.1 概述
      2. 6.1.2 经典运用
    2. 6.2 变治算法
      1. 6.2.1 概述
      2. 6.1.2 经典运用
数据结构与算法 计算机组成原理 计算机网络 汇编语言 数据的存储与传输 操作系统 互联网标准RFC 编译链接与装载 iOS 架构与设计模式 图形处理与渲染 软件工程 音视频处理 DSL Swift Git Web
Total : 75
搜索
2022
2021
2020
AutoreleasePool hexo GCD ISA Microarch Soc 多线程 CLI Shell ARM64 Docker DSL 协程 Fiber dp SwiftUI RunLoop Swift-Syntax LagMonitor CrashMonitor Log AFN